Определите силу натяжения резинового кольца (29 января 2008)

FatherTorque - 29 января, 2008 - 12:01
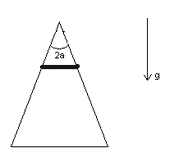рисунокИз тонкого резинового шнура длиной Lo и массой m изготовлено кольцо. Его надели на гладкий конус с углом 2α при вершине. Определите силу натяжения, возникающую в кольце. Площадь поперечного сечения шнура S и модуль Юнга для резины E считать известными.

Задача взята из контрольных работ подготовительного курса учебного центра "Ориентир". Примерный рисунок нарисован в Paint.

Теги:

Комментарии

Опубликовано 29 января, 2008 - 22:30 пользователем В. Грабцевич
Подсказка: выберем малый элемент шнура, видимый под малым углом β с центра окружности, которую описывает шнур. Расставим силы, действующие на малый элемент: сила тяжести, сила упругости шнура, сила реакции опоры поверхности конуса. Так как ситуация статичная, то выполнится условие равенства нулю векторной суммы приложенных сил к элементу. Выберем оси координат: ось OX направим по радиусу окружности шнура, ось OY перпендикулярно. Далее найдите проекции силы на выбранные направления. Вам понадобится уравнение, связывающее радиус с длиной дуги малого элемента, и понятие, например, линейной плотности массы шнура. Решая полученные уравнения совместно, придете к искомому результату.

Примечание: синус малого угла равен самому углу, выраженному в радианах, учтите изменение длины шнура при деформации.

Опубликовано 4 февраля, 2008 - 18:25 пользователем FatherTorque
Этот метод решения уже рассматривался, он не работает в данном случае. Согласитесь, он нестандартный для этой задачи. Я точно не помню в чём там загвоздка, но в скором времени попробую выложить решение.(вроде бы кол-во неизвестных не совпадает с кол-вом уравнений).
Опубликовано 4 февраля, 2008 - 19:27 пользователем В. Грабцевич
Решил задачу, используя свои подсказки, получил конечную формулу, в которой используются все данные задачи. Если не получится решить, сообщите, я выложу свое решение.

Примечание. По ходу решения возникает уменьшение площади поперечного сечения жгута, при его удлинении, что отражается на жесткости, если этим эффектом пренебречь, то проблем не возникает (считать что k = ES/lo). Если учитывать изменение жесткости, то решение усложняется, но все же выход на конечную формулу есть.

Внимательно рассмотрю Ваше решение. Спасибо.

Опубликовано 6 февраля, 2008 - 17:40 пользователем FatherTorque
Хорошо. Выберем малый элемент шнура, почти точку или малый шар. На него действует вертикально вниз сила тяжести mg, от него к центру окружности направлена сила упругости (правильно понимаю?), а сила реакции опоры, т.е. конуса, направлена от шара перпендикулярно поверхности конуса (верно?) — наружу.

Тогда в проекции на ось X:
Fупр − Nsin (2α) = 0;
ось Y:
Ncos (2α) − mg = 0.

Выражаем отсюда силу упругости, получается Fупр = mg*tg (2α).
Если брали один элемент, находящийся в единице длины, то логично предположить, что сила упругости для всего шнура, т.е. для всех "элементов" равна:

FупрL = Fупр.общ. (в дальнейшем просто Fоб.). <з>Эта же Fоб = k(L − L0) = ES(L − L0)/L0.

Итак, 2 уравнения, 2 неизвестных (L и Fоб.). Решая систему, получаем конечный ответ:

F = mgSE*tg(2α)L0 / (SE − mg*tg(2α)L0)

Жду ваших замечаний. Огромное спасибо за помощь.

P.S. кстати, еще есть рисунок новый, но я что-то опять не могу найти кнопочки "добавить файл".

Отредактировано afportal 6.02.08.
Добавлять рисунки (не любые файлы) можно при размещении задачи. В остальных случаях присылайте рисунки мне. E-mail указан в блоке "Помощь по HTML", который виден в левой колонке под ссылками при добавлении и редактировании комментариев.

Опубликовано 6 февраля, 2008 - 20:19 пользователем В. Грабцевич
рисунок 1 Выберем малый элемент шнура. На него действует вертикально вниз сила тяжести Δmg, от него к центру окружности направлена результирующая сила упругости, а сила реакции опоры, т.е. боковой поверхности конуса направлена от элемента шнура перпендикулярно поверхности конуса.

Тогда в проекции на ось X, направленную к центру окружности шнура, будет:

Fупр х − N×cos α = 0,

в проекции на ось Y:

N × sin α − Δmg = 0.

Выражаем отсюда силу упругости, получается:

Fупр х = mg/tg α.

рисунок 2Учтем, что Fупр х = 2T × sin (β/2) = T × β (в силу малости угла β )

Тогда T × β = Δmg/tg α.     (1)

Используя связь радиуса и длины дуги R × β = Δl, выразим β и заменим в уравнении (1).

У нас появился радиус окружности жгута, он связан соотношением:

lo + Δx = 2πR.

И еще, kΔx = Tlo/(ES) , и Δm/Δl = m/lo — линейная плотность жгута.

Если теперь все собрать и перегруппировать относительно искомой T, получим:

T = mg/(2πEStg α − mg).