При каком коэффициенте трения ящик опрокинется? (8 августа 2009)

AssemblerIA64 - 8 августа, 2009 - 20:07
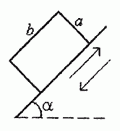На неподвижной ленте транспортёра, наклонённой под углом ? к горизонту, лежит ящик размерами a ? b. Лента трогается с места с очень большим ускорением. При каком значении коэффициента трения ящик опрокинется? Рассмотреть случаи движения ленты вверх и вниз.

Источник: Задачник, раздел 17.1 (статика), № 17.18.

Теги:

Комментарии

Опубликовано 8 августа, 2009 - 21:01 пользователем AssemblerIA64
Размещу на всякий случай своё неправильное решение.

Векторные суммы всех сил, действующих на тело, и моментов этих сил должны быть равны нулевому вектору.

Запишем проекции сил:

x:   Fтр − Fин − mg sin ? = 0     (1).

y:   N = mg cos ?.

Теперь проекции моментов сил относительно точки А на ось, перпендикулярную плоскости рисунка:

Fинa/2 + Nb/2 − mg (b/2 − (a tg ?) / 2) cos ? = 0.

Fинa + mg (cos ?) b − mg (b − a tg ?) cos ? = 0.

Отсюда:

Fин = −mg sin ?     (2).

Подставляем (2) в (1):

Fтр = mg sin ? − mg sin ?, т.е. ? = 0, а в ответе должно быть ? > b/a.

Опубликовано 10 августа, 2009 - 09:58 пользователем inkerman
Рисунок неверный. Сила N приложена к т. А.

Задачу лучше решать в инерциальной системе. Иначе будет ненужная путаница.

Опубликовано 11 августа, 2009 - 21:57 пользователем zvv48
Сила N приложена не в точке А, а в точке пересечения линии действия силы тяжести и наклонной плоскости.
Опубликовано 12 августа, 2009 - 10:07 пользователем inkerman
Если бы брусок не переворачивался — да. А тут он переворачивается вокруг т. А. Поэтому N приложена к т. А.
Опубликовано 12 августа, 2009 - 12:50 пользователем zvv48
Мне не понятно, почему он должен переворачиваться. Если сила N проходит через точку А, линия действия силы трения тоже проходит через А, а сила тяжести создаёт момент по часовой, то что тогда?
Опубликовано 12 августа, 2009 - 14:25 пользователем inkerman
Читаем условие: НУЖНО, чтобы перевернулся. Ищем условия, при которых перевернется.

Ответ на Ваш вопрос: не перевернется, и сила N тогда будет не в т. А., но ведь нужно, чтобы перевернулся! Поэтому будет в т. А. а момент будет против часовой (ну или хотя бы 0).

Опубликовано 12 августа, 2009 - 17:34 пользователем zvv48
Опять не понятно. Когда сила N в точке А, то она не создает момента. А какая сила поворачивает против часовой стрелки? Я думаю, что момент создаст сила N (точнее, импульс силы N!), когда она находится не в точке А, а ранее. В тот момент, когда сила трения достигает максимума.
Опубликовано 12 августа, 2009 - 20:46 пользователем inkerman
Импульс N? Я таких способов решений подобных задач не видел, хотя я ведь и не преподаватель, поэтому Вы, как препод, вероятно, имеете более богатый опыт. Если не сложно — покажите, как бы Вы решали через импульс N.

Я бы решал относительно центра масс. Расписал бы силы и показал что сила реакции (N + Fтр) должна проходить через ЦМ, откуда получим ответ.

Опубликовано 12 августа, 2009 - 21:48 пользователем zvv48
Я учитель, а не преподаватель. Пока не вижу правильного решения. Из термеха следует, что за ось вращения можно выбрать любую точку плоскости. Относительно ЦМ ответ получается, а относительно А нет. Я проконсультируюсь у спецов, тогда и напишу.
Опубликовано 12 августа, 2009 - 23:09 пользователем inkerman
Насколько я помню, ось можно выбирать любую в системе центра масс.
Опубликовано 13 августа, 2009 - 09:20 пользователем zvv48
За ось можно выбрать любую ось, проходящую перпендикулярно плоскости в любой точке чертежа.
Опубликовано 13 августа, 2009 - 12:01 пользователем inkerman
Вы заблуждаетесь.

Ось можно выбирать любой, если и только если в данной СО сумма всех внешних сил равна нулю. Только в этом случае суммарный момент не будет зависеть от выбора оси.

В выбранной ИСО (Земля) сумма всех сил не равна 0. И суммарный момент зависит от оси, что мы и наблюдаем собственно на примере этой задачи.

Опубликовано 13 августа, 2009 - 23:14 пользователем zvv48
Правильно, Юра! МФТИ — это супер! Но в ответе этой задачи должен входить угол α.
α → 0 — один ответ, α → 90° — другой.

Спасибо за подсказку! Это не такая уж простая задача! Она имеет промышленное значение (сегодня читал в инете о таком понятии как "Конус трения"!)

Например, транспортёрная лента, стеклянные бутылки — при трогании они могут опрокинуться. Или в Мюнхене по этой причине рухнул мост.

Ответ μ > b/а дан для случая горизонтального расположения бруска (это простейший случай). Решение следует из двух уравнений: Mин > Mmg и Fин < Fтр. Ось вращения в т. А.

Опубликовано 14 августа, 2009 - 07:14 пользователем inkerman
Fин < Fтр.
Не совсем понял, куда исчезла проекция mg.

Вобщем-то я с ответом согласен. Для любого угла. Если Вы готовы показать более правильное решение, опубликуйте его, и мы вместе его обсудим.

P.S. Не понял, чем вызвал такую радость по поводу МФТИ, но все равно приятно. Спасибо.

Опубликовано 14 августа, 2009 - 09:13 пользователем AssemblerIA64
Спасибо, получилось!
Опубликовано 14 августа, 2009 - 10:28 пользователем inkerman
Что получилось-то? Решили и с ответом сошлось? Ну так поделитесь Вашим решением!
Опубликовано 14 августа, 2009 - 12:40 пользователем Успех
Такое решение показывывает, что тело должно соскальзывать, а не опрокидываться через ребро.
Опубликовано 14 августа, 2009 - 13:01 пользователем inkerman
какое такое?
Опубликовано 14 августа, 2009 - 13:54 пользователем AssemblerIA64
Сошлость. Решение такое же, как и в первом сообщении, только N и Fтр приложены к точке A.